Astronomical units of measurement
This article explains the specification of distances, angles and magnitudes in an astromic context.
Distances
The unit commonly used in everyday life Kilometers is generally only used for short distances, e.g. for planetary diameters or the average distance from the earth to the moon of 384,400 km. If it goes beyond this, the term astronomical unit is used.
One Astronomical unitalso abbreviated to AE or au, is the average distance from the Earth to the Sun. This is 149,597,871 kilometers. You can see that the use of km is already impractical here. Accordingly, the AU was introduced. This unit is usually used within the solar system. The distance to the nearest star Proxima Centauri is already 270000 AU, which also quickly becomes impractical. The light year is used here.
With the Light year (abbreviation LJ or ly) is not a measure of time, as might be assumed, but a measure of distance. A light year is the distance that light travels in a vacuum at a speed of 299,792 km/s within one year. The distance to Proxima Centauri is therefore around 4.246 LJ, that of the moon just under 1.3 light seconds.
Parsecparallax second (abbreviation pc), is used for even greater distances. A parsec is defined as the distance at which one AU, i.e. the average distance from the earth to the sun, appears at an angle of one arc second (1"). This is the case at a distance of around 3.2615 LJ. Parsec is also used with the suffix kilo or mega. So kpc or Mpc.
Angle
In astronomy, the common units for angles are used. These consist of Degree (abbr. °), arc minutes (abbr. ') and Arc seconds (abbr. "). One degree consists of 60 arcminutes, one arcminute of 60 arcseconds. One second of arc is therefore 1/3600 of a degree. This resolution, i.e. the angle at which two objects can still be optically recognized as separate from each other, can certainly be achieved with medium-sized amateur telescopes under good viewing conditions, also known as "seeing" in astronomy. The moon and sun, for example, have an average optical diameter of around 30' or 0.5° in the sky.
The following method can be used to roughly estimate the angles in the sky: The distance between the tip of the thumb and the tip of the middle finger of a fully spread hand of an adult, held at arm's length away from the body, is roughly 15°. The width of a fist across the knuckles is approximately 7°. The diameter of the tip of the little finger at arm's length is approximately 1°.
Brightnesses
Apparent brightness of stars or other celestial bodies are measured with Magnitude (abbr. may or m). Occasionally the term magnitude class or size is also used. The lower the value, the brighter the object. Here are some examples:
Sun: -26.7mag
Full moon: -12.7mag
Venus at maximum brightness: -4.4mag
Jupiter at maximum brightness: -2.9mag
Sirius, brightest star: -1.46mag
The brightness curve is not linear, i.e. it does not graphically correspond to a line, but changes by a factor of 2.51 per magnitude class. A star of 2mag is therefore 2.51 times brighter than a star of 3mag.
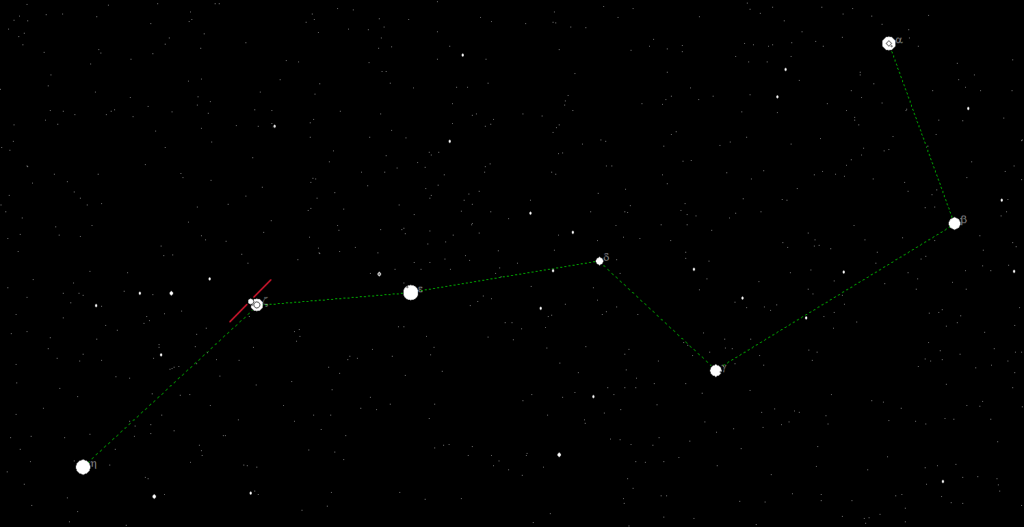
A practical application is used to estimate the quality of the night sky. If the star Alkor is visible at 4mag, directly to the left above the central pole star of the "Big Dipper", the visibility of stars is quite reasonable. Due to the light pollution in our latitudes, a value of 5 to 6mag is rarely achieved. Incidentally, due to its proximity to the star Mizar, Alkor is often referred to as "The Little Rider".
Occasionally, the terms "absolute brightness" and "surface brightness" are also used. These are not relevant for simple practical observation and are discussed in detail in other sources.